By: Richard W. Sharp
The scores are in and the nets are down. North Carolina is champion for the sixth time, and Gonzaga has played its first final. In what must surely be an unprecedented conclusion, two top ranked teams met and after a hard fought contest last year’s runner up came out on top. Who could have predicted that?1 Nobody knew that [NCAA brackets] could be so complicated.
Well, OK, maybe we’ve been concentrating a little too hard on upsets the last couple weeks. Anyway, it’s April now. Time to let sanity settle back in and review our approach: Did a dash of randomness help boost a reasonable fraction of our brackets high up the leaderboard? Would we expect the approach to translate into winning some pools over the years or is it time to modify our strategy for next year?
Let the second-guessing begin!
The short-short version
How’d our applied randomness do? Comparing to the stand-alone bracket results, the most we can claim is that if you picked one of the high performing randomized brackets, then you should be in striking distance within your pool. The randomized approach seems to have merit, but there’s still some work to do for it to become a consistent winner.
Checking in: Stand-alone brackets
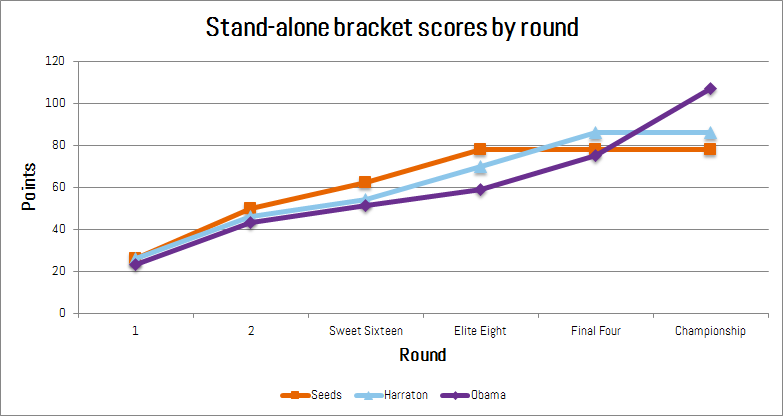
First, let’s check in with the stand-alone brackets to see how they fared.
- Sagarin with mascot weighting #14
- Source: Our randomly selected mascot randomized bracket: bracket.ranker_SAG.mascot_14.csv2
- Total points: 63
- What happened: After early success, sank like a rock to the bottom of the pool.
- RPI
- Source: Rating Percentage Index, used in part to select teams for the tournament
- Total points: 66
- What happened: Was chained to SAG 14 as it went down.
- Straight Seeds
- Source: The official tournament seeds, combined with AP Top 25 to select Final Four and Championship winners.
- Total points: 78
- What happened: Villanova lost. As usual, the pre-tourney favorite failed to go all the way.
- Harraton
- Source: Harraton, who will now lord it over me.
- Total points: 86
- What happened: PNW bonus – chose Gonzaga and Oregon for Final Four.
- Obama
- Source: The former president.
- Total points: 107
- What happened: Knows how to pick a winner, in this case, UNC.
- Actual pool winner
- Source: Actual pool that SAG 14 and Harraton (placed 3rd) took part in.
- Total points 122
- What happened: PNW bonus, 3/4 final four, correct championship matchup
- Final Four
- Villanova vs. Gonzaga
- Oregon vs. North Carolina
- Championship
- Gonzaga defeats North Carolina
- Final Four
- Top randomized bracket
- Source: a tie between two of our purely random brackets: Bihl (BIH) 4.0 #89 and Sport Theory (STH) 4.0 #6
- Total points: 154
- What happened: 3/4 final four with UNC to beat Gonzaga
- Final Four
- Villanova vs. Gonzaga
- Oregon vs. North Carolina
- Championship
- North Carolina defeats Gonzaga
- Final Four
Checking in: Randomized Brackets
While some of the best individual bracket results are impressive, it’s the randomized brackets that are supposed to help us win the pool. Recall that we used two different randomization approaches: one based on our own, completely subjective mascots ranking, and a second that used true random noise. In both cases the noise was added to base rankings from each of 27 established ranking systems.3 The idea was that, while you won’t win every year, a significant fraction, say one-in-ten of the randomized brackets should perform very well. You should expect to win a pool every now and then. So how did the approaches fare? Below, we’ve ranked the different approaches by aggregating all brackets from each randomization scheme and determining the 90th percentile bracket score within each segment: one-in-ten of the brackets produced by this approach have done at least this well.
- Aggregate results
- Mascots
- 90th pct: 92
- High score: 141
- Most common championship above 90th pct: UCLA defeats Villanova
- Random stdev = 4
- 90th pct: 108
- High score: 154
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Random stdev = 5
- 90th pct: 105
- High score: 150
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Random stdev = 6
- 90th pct: 107
- High score: 153
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Mascots
There was a clear winner in the individual ranker contest: Dr. Entropy, the only method to correctly place UNC atop the field at the outset of the tournament, as well as having Gonzaga at #2. As with the aggregate results, mascots based randomization did not work as well as true randomization.

Dr. Steel, probable father’s brother’s nephew’s cousin’s former roommate to Dr. Entropy.
- Best Individual Ranker: Doktor Entropy (DOK)
- Mascots
- 90th pct: 139
- High score: 141
- Most common championship above 90th pct: North Carolina defeats Villanova
- Random stdev = 4
- 90th pct: 138
- High score: 147
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Random stdev = 5
- 90th pct: 134
- High score: 143
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Random stdev = 6
- 90th pct: 138
- High score: 152
- Most common championship above 90th pct: North Carolina defeats Gonzaga
- Mascots
What about the other individual rankers? The table below ranks the rankers based on the 90th percentile score of their true random stdev 5 results. SAG, the ranker we based our pool picks on did respectably, tied for 10th of 27 (note that the bracket entered in the pool was based on mascot generated noise). SAG probably benefitted from having Gonzaga at number 1 and UNC 4th, thus setting up some good Final Four and Championshi scenarios. Several rankers did better, especially DOK, which had UNC at #1. On the other hand RPI demoted the Zags to 10th4 although it also had UNC in 4th. It finished near the bottom as usual: tied for 21st of 27.
| Ranking the models: How did they do in 2017? | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | Ranker | 90th pct | |||||||
| 1 | Doktor Entropy (DOK) | 134 | |||||||
| 2 | Daniel Curry Index (DCI) | 126 | |||||||
| 3 | Whitlock (WLK) | 124 | |||||||
| 4 | RoundTable (RT) | 121 | |||||||
| 5 | Wilson (WIL) | 113 | |||||||
| 6 | Kirkpatrick (KPK) | 112 | |||||||
| 7 | Cheong (CNG) | 111 | |||||||
| t8 | Dance Card (DC) | 109 | |||||||
| t8 | Pomeroy (POM) | 109 | |||||||
| t10 | Pugh (PGH) | 108 | |||||||
| t10 | Sagarin (SAG) | 108 | |||||||
| 12 | Moore (MOR) | 101 | |||||||
| 13 | Dolphin (DOL) | 99 | |||||||
| 14 | Wolfe (WOL) | 98 | |||||||
| t15 | LRMC (LMC) | 97 | |||||||
| t15 | Rothman (RTH) | 97 | |||||||
| t17 | Colley (COL) | 95 | |||||||
| t17 | Sport Theory (STH) | 95 | |||||||
| t19 | Massey (MAS) | 94 | |||||||
| t19 | Krach (KRA) | 94 | |||||||
| t21 | RPI (RPI) | 93 | |||||||
| t21 | Bihl (BIH) | 93 | |||||||
| t23 | Wobus (WOB) | 92 | |||||||
| t23 | Rewards (REW) | 92 | |||||||
| 25 | Pigskin (PIG) | 91 | |||||||
| 26 | Snapper’s World (SPW) | 86 | |||||||
| 27 | Nolan (NOL) | 81 | |||||||
Finally, there was a two-way tie for the ranker that produced the best overall bracket between Sport Theory (SIH) and Bihl (BIH). However, these appear to have been one-off lucky brackets, since the respective 90th percentile scores lag the aggregate result. Note that while both get the championship matchup correct, Gonzaga is usually favored, even though we’ve biased the sample by focusing on the best performing brackets.
- Best overall bracket
- Sport Theory (STH) – Random stdev = 4
- 90th pct: 98
- High score: 154
- Most common championship above 90th pct: Gonzaga defeats North Carolina
- Bihl (BIH) – Random stdev = 4
- 90th pct: 104
- High score: 154
- Most common championship above 90th pct: Gonzaga defeats North Carolina
- Sport Theory (STH) – Random stdev = 4
So how about our randomized bracket strategy? Comparing to the stand-alone bracket results, the most we can claim is that if you picked one of the high performing randomized brackets, then you should be in striking distance within your pool. Unless you were in a pool with a Portland transplant from South Carolina. The randomized approach seems to have some merit, but there’s still some work to do for it to become a consistent winner.
To get some ideas for next year, let’s pick apart the come-from-behind champion among our original stand-alone brackets: President Obama’s.
Why Evil Obama’s tax bracket took your money, even after he left office
The clear and obvious reason for Obama’s success is that he is indeed a Kenyan Muslim supervillian capable of bending the laws of mathematics to his will. Well, that or the decidedly less exciting non-alternative fact that he picked North Carolina to win it all.
Obama has, at best, a mixed record with bracket picking. But, as the pundits have pointed out, he was busy. Bracketeering, it seems, is a full time job.
Picking the overall winner is (shockingly) pretty important given the scoring system we considered. Recall that 1 point is awarded for each correct pick in the first round, and the point value for each correct pick doubles in each successive round (six in total). So the winner is worth 1 + 2 + 4 + 8+ 16 + 32 = 63 points, or 33% of the 192 possible points.
In the end, picking North Carolina was the one thing that did go right for Obama’s bracket. Going into the Final Four, his bracket was last among our stand-alone brackets with 59 points. North Carolina was his only correct Final Four pick.
- Duke (2) vs. Arizona (2)
- Kansas (1) vs. UNC (1)
In fact, he had earned all 44 of his non-UNC points by the third round.
Obama’s coming for your bracket.
Time to play “What if?”
Is this all there is to it? Are there other factors that help build a strong bracket? What if you had picked the big upsets? With teams like South Carolina and Xavier going deep into the tournament, you might expect to have been handsomely rewarded for picking them. Your prescience would have earned you points in matchups where most others didn’t even have a horse in the race. Maybe this can help you overcome picking Villanova to take it all.
- What if you picked straight seeds but with South Carolina going to the Final Four?
- 78 + (2 + 4 + 8) = 92, Obama wins
- What if you picked straight seeds but with South Carolina going to the Final Four and Xavier to the Elite Eight?
- 78 + 14 + (1 + 2+ 4) = 99, Obama wins
- What if you picked straight seeds but with South Carolina and Oregon going to the Final Four and Xavier to the Elite Eight?
- 78 + 14 + 7 + (8) = 107, Obama wins by tiebreaker (chose the champ)
- What if you picked 3/4 final four teams and the correct championship match, but had Gonzaga going all the way?
- 122 points, the winner of the pool that the SAG 14 bracket was entered into, and the only organic bracket I’ve come across that’s beaten the Obama bracket without picking UNC.
Finally, what if you picked straight seeds with North Carolina as champion? That would be worth 78 + (16 + 32) = 126 points, a decisive winner vs. Obama.
In the end, Obama did a great job of picking upsets by picking a lot of upsets and these got him in trouble early. He salvaged his bracket by making one incisive pick. Dumb luck? Not likely, at least it wasn’t just on a whim considering he correctly placed North Carolina in the championship last year as well.
Strategy Update
We opened this series with the assertion that playing straight seeds was a recipe for second place. By adding a degree of randomness to the selection process we would, from time to time, get lucky and select a superior bracket. How much randomness was the right amount? Should we bias the random choices in an arbitrary manner so that at least our bracket would stick out from the crowd (for better or worse)? Well, our approach, while respectable, didn’t exactly blow away the field.
So, how should we adapt next year?
The big change, clearly has to be giving more weight to the selection process in the final rounds. Of course this only applies to the scoring system we chose in which correct picks in each round are worth double the previous round’s score. So much emphasis is placed on picking the overall winner (1/3 of the total points possible) that Obama’s bracket, despite all its struggles in the opening rounds, would be a serious contender in any bracket geographically and alumnietically5 distinct from the Carolinas or Cascadia.
In the men’s tournament, it is rare that the pre-tournament favorite wins the title. In fact, only one of the 27 rankings we considered did so, and 538 gave UNC only a 15% chance of winning it all. Whatever approach is used, careful consideration must be applied to the final rounds. Randomness should not be given equal weight here.6, 7
There is, however, an advantage to picking an unpopular champion. If you pick the favorite, and the favorite wins, then you will need other wins for your bracket to stand out. Choosing a less common overall champion gives you the double bonus of high points and less competition in your pool – if you’re playing the long game, year after year. In any event, March Madness decidedly does not reward rationality (go Northwestern!).
Specifically picking upsets does not create a winning bracket on its own. Compared to straight seeds only South Carolina was likely to move the needle (+14 points). Even picking Oregon only gives you a +8 bonus. Of course, another path to 2/4 in the Final Four this year was picking all of the #1 seeds. Even picking the big losers won’t help. Having Villanova crash out was only worth +5.
So we’re left with the question: how much randomness is the right amount? The best result in this year’s contest came from using stdev = 4, a bit lower than in years past. However, this was barely distinct from higher levels. Further study is required.
Another question we will take up in our next post is how to adapt our approach for the Women’s tournament. The single most significant game in NCAA basketball this year was between UConn and Mississippi St. in the women’s Final Four. Mississippi St. won, denying UConn a fifth consecutive championship. In fact, upsets in general were far less common than in the men’s game. The approach will at least need to be re-calibrated, or perhaps a new one will need to be built.
In any case, time to let the fever dreams of March subside, return to sanity, and prepare for tax day.
1 Apparently Dr. Entropy can, the only ranker considered that selected UNC #1 overall (with Gonzaga #2). I also don’t fancy my chances against Michael Jordan’s bracket.^
2 This was the one that really mattered, we entered it in a pool. Unfortunately it floundered there, and had the pants beaten off of it by Harraton’s bracket.^
3 We did not use all of the rankings collected by massyratings.com, only those with several years of historical records.^
4 ??!!^
5 This is not a real word, but it should have been because I need it.^
6 Actually, even with our approach, the effect of randomness diminishes the deeper into the tournament you go. That is, a #1 seed, which only has to avoid being very unlucky, is still far more likely to make it to the championship than a #16 seed, which has to get lucky in each of 6 rounds. The suggestion here is to consider an even more restrictive approach to random factors in later rounds.^
7 Interesting fact, shift your left hand to the left by one column of keys and “foot” becomes “door”. There’s a pub-quiz question in this somewhere.^


No Comments on "Applied bracketeering wrapup: Highly-rated team wins in shocking finale"